Calendarium : Измерение времени и календарь

В главе "Экваториальная система координат" уже было введено понятие звездного времени как часового угла точки весеннего равноденствия. Соответственно, звездные сутки определяются как интервал времени между двумя последовательными верхними кульминациями точки весеннего равноденствия. Равномерность звездного времени определяется только равномерностью вращения Земли, о чем будет рассказано ниже. Однако для повседневной жизни звездное время непригодно, так так Солнце смещается по эклиптике, из-за чего время верхней кульминации точки весеннего равноденствия в течение года смещается относительно времени верхней кульминации Солнца и поэтому бывает в разное время суток, а звездные сутки короче солнечных на 3^м 56^с.55. Для выражения меньших промежутков времени звездные сутки делят на 24 звездных часа, час - на 60 звездных минут, минуту - на 60 звездных секунд. Поскольку небесная сфера совершает полный оборот за 1 звездные сутки, то за 1 звездный час она поворачивается на 15^o, за минуту - на 15', за секунду - на 15". Как уже упоминалось, прямое восхождения светила aи его часовой угол t связаны со звездным временем s простым соотношением:

В отличие от звездного времени, солнечное соответствует требованиям повседневной жизни, но определить его гораздо сложнее. В главе "Эклиптическая система координат" было дано определение истинного солнечного времени как часового угла Солнца и истиных солнечных суток как промежутка времени между двумя истиными полуднями. Однако поскольку земная орбита - эллипс, то вблизи перигелия (в начале января) скорость Земли максимальна и за истинные солнечные сутки она смещается на 61'.1 по отношению к направлению на Солнце, вблизи афелия (в начале июля) - всего на 57'.2. Поэтому истинные солнечные сутки зимой длиннее, а летом - короче. Неравномерность истинных солнечных суток вследствии эллипсичности земной орбиты можно представить синусоидой с амплитудой 7.6 минут и начальной фазой в перигелии 4 января.

Кроме того, вследствии наклона эклиптики к экватору равные участки эклиптики, по которым движется Солнца по небесной сфере, в проекции на экватор дают неравные отрезки, что также вносит вклад в неравномерность истинного солнечного времени. Эту неравномерность можно представить синусоидой с амплитудой 9.8 минут, периодом полгода и начальной фазой в день весеннего равноденствия.

С целью получения равномерного солнечного времени было введено понятие "среднего солнца" - некоторой фиктивной точки, равномерно движущейся по небесному экватору в том же направлении, что и реальное Солнце, с периодом 1 год (~365.2422 суток). По аналогии со звездным временем, часовой угол этого "среднего солнца" определяет среднее солнечное время, а промежуток времени между двумя последовательными верхними кульминациями "среднего солнца" - средними солнечными сутками. Сам момент верхней кульминации "среднего солнца" (средний полдень) до 1925 года принимался за начало средних солнечных суток, а с 1 января 1925 года по по международному соглашению считается равным 12 часам, поскольку начало календарных суток приходится на ночь. Средние солнечные сутки сохраняют постоянную продолжительность. Нетрудно подсчитать, что прямое восхождение среднего солнца возрастает в сутки на 360^o/365.2422 = 0^o.98564 ~ 3^м 56^с.55. Поэтому солнечные сутки длиннее звездных именно на такую величину. Если обозначить часовой угол среднего солнца через t_m, то среднее солнечное время можно определить как T_m = t_m + 12ч.

Чтобы связать истинное и среднее времена, выразим для некоторого момента звездное время через часовой угол и прямое восхождение истинного Солнца s = t_s + a_s и среднего солнца s = t_m + a_m. Приравняв оба выражения, получим:

Разность h = a_s- a_m называется уравнением времени. На основании известных закономерностей движения Земли эта величина может быть заранее вычислена для любого момента времени. Поэтому среднее время T_m можно получить, измерив часовой угол истинного Солнца t_s, прибавив к нему соответствующее значение h и 12 часов:

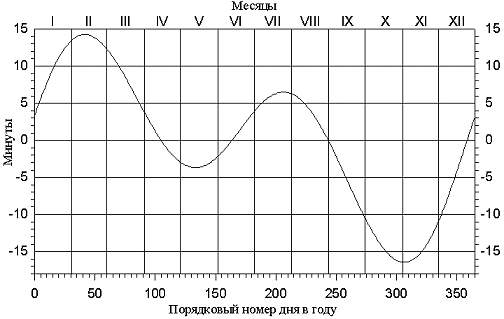
Рис. 1. График уравнения времени для 2000 года. Получен по данным программы - планетария XEphem 3.1.

График уравнения времени для 2000 года приведен на рис. 1. Для других лет он будет иметь такой же вид, только возможны небольшие (на 1-2 дня) смещения по горизонтальной оси из-за того, что солнечный год не содержит целого числа суток.

Приближенное значения уравнения времени в зависимости от номера n дня в году можно получить как разность двух описанных выше неравномерностей длины истинных солнечных суток:

Первое слагаемое учитывает неравномерность движения Земли по орбите (4 - порядковый номер дня прохождения перигелия, соответствующего примерно 4 января), второе - проекция на экватор движения Солнца по эклиптике (множитель 0^o.986 удвоен, поскольку период составляет полгода, а 81 - номер дня весеннего равноденствия).

В течение года значение h четыре раза обращается в ноль (около 15 апреля, 14 июня, 1 сентября и 25 декабря) и четыре раза достигает крайних значений (11 февраля, 15 мая, 26 июля и 3 ноября, соответственно +14.3 мин, -3.7 мин, +6.4 мин и -16.4 мин). Быстрее всего (до 30 с в сутки) уравнение времени изменяется в декабре, что вызывает интересное явление. Известно, что самый короткий день в году (в северном полушарии) бывает в день зимнего солнцестояния, 22 или 23 декабря. Однако по эфемеридам Солнца можно найти, что для Москвы самый ранний заход Солнца приходится на середину декабря, а самый поздний восход - на конец декабря. Объясняется это так. До солнцестояния, когда продолжительность дня медленно уменьшается, это уменьшение происходит и утром, когда восход Солнца запаздывает, и вечером, когда Солнце раньше заходит. Моменты восхода и захода симметричны относительно истинного полдня, но ежедневно запаздывают относительно среднего времени. Поэтому перед днем зимнего солнцестояния запаздывание восхода Солнца складывается из-за действительного запаздывания (вследствие уменьшения его склонения) и сдвига истинного полдня на более позднее время. Вечером же смещение истинного полдня действует против действительного более раннего захода Солнца. В результате восход Солнца по среднему времени запаздывает еще на несколько дней после солнцестояния, а вся начавшаяся прибавка дня приходится на более поздний заход вечером.

Верхняя кульминация среднего солнца (средний полдень) наступает одновременно для всех точек, лежащих на одном земном меридиане. Из-за вращения Земли эта зона смещается с востока на запад со скоростью 15^o в час. В результате каждый меридиан имеет свое среднее солнечное время, которое зависит от его долготы. Это время называется местным среднем временем. Среднее местное время нулевого меридиана, за который принят меридиан, проходящий через пассажный инструмент Гринвичской обсерватории (на восточной окраине Лондона), называется всемирным временем (а также мировым или Гринвичским) и обозначается UT или МВ. Разность местных времен на меридианах с географическими долготами l_A и l_B будет равна промежутку времени, необходимому для для поворота Земли на угол между плоскостями меридианов l_A и l_B, то есть на разность долгот. Поэтому на более западном меридиане среднее время будет меньше на величину Dl = l_A - l_B. Поэтому местное среднее время T_m на меридиане с долготой l (положительной к востоку от Гринвича) будет на величину l больше всемирного времени T₀:

Теперь можно связать звездное время со средним местным T_mи всемирным T₀. Если обозначить через s₀ звездное время на меридиане Гринвича в 0 часов всемирного времени (звездное время в среднюю гринвичскую полночь), а через s - местное звездное время на долготе l, то

В выражениях (5) и (6) коэффициент 9^c.86 - это величина изменения звездного времени за 1 час среднего солнечного (9^c.86 * 24 = 3^м 56^с.6), поэтому заключенные в скобки значения T₀ и T_m - l должны быть выражены в часах и десятичных долях часа. Значения s₀ на каждые сутки приводятся в астрономических ежегодниках, например, в астрономических календарях.

Однако местное среднее время также неудобно в гражданской жизни, так как каждый город должен был жить по своему времени, что затрудняет сообщение между ними. В странах, не сильно растянутых по долготе, можно было считать единое время, обычно совпадающее с местным временем столицы. Так было, например, в Англии, Франции, Германии и ряде других небольших стран. Но для стран, имеющих большую протяженность по долготе, такое решение не подходило. Поэтому было введено поясное время, для чего весь земной шар был поделен на 24 часовых пояса, каждый - 15^o по долготе, причем центральный меридиан нулевого пояса совпадает с Гринвичским меридианом. Счет поясов ведется к востоку, поэтому долготы центральных меридианов часовых поясов кратны 15^o(0^o, 15^o, 30^o, ...), а их границы отстоят на 7^o.5 к востоку и западу от центрального меридиана (0-й пояс - от 352^o.5 до 7^o.5, 1-й пояс - от 7^o.5 до 22^o.5, 2-й - от 22^o.5 до 37^o.5 и т.д.). Внутри каждого пояса время считается единым и равным местному среднему времени центрального меридиана. Таким образом было достигнуто, что время разных часовых поясов отличается на целое число часов, равное разности номеров поясов.

На практике границы часовых поясов проведены не строго по указанным долготам, а применительно к границам государств, а внутри стран - по административным границам и природным образованиям - горным хребтам и большим рекам. Иначе пришлось бы делить на части области, районы, а иногда - и города. Например, большая часть Москвы (l = 37^o 42') попала бы в третий пояс, а ее западные пригороды оказались бы во втором. Поэтому для удобства вся Москва и Московская область отнесены ко второму поясу, куда также входит Петербург и вся западная часть России. В СССР счисление времени по часовым поясам было введено в 1919 году и на его территорию (как и современную Россию) приходится 11 часовых поясов.

Местное солнечное время и, в частности, поясное время, согласованы с вращением Земли, однако они не привязаны к конкретным календарным датам. Поскольку географическая долгота неисчерпаема, то, например, перемещаясь на запад, в соответствии с требованиями поясного времени, примерно каждые 15^o нужно переставлять часы на один час назад, то есть после пересечения (неважно, за какой срок) всех 24 поясов вернемся в исходный часовой пояс, но получим дату, предшествующую текущей "местной" дате. Впервые такое явление было отмечено участниками первой кругосветной экспедиции Магеллана (XXVI век), чем сильно их озадачило. Для устранения путаницы в датах было достигнуто международное соглашение о введении линии перемены дат (демаркационной линии), на которой начинается новая дата. Чтобы не причинять новых неудобств, эта линия проведена примерно по географическому меридиану с l = 180^o, по пустынным областям Тихого Океана, немного отклоняясь от этой долготы около юго-восточной Азии и нескольких групп островов. При пересечении демаркационной линии с запада на восток предписано уменьшать календарное число (и день недели) на единицу, а при пересечении с востока на запад - увеличить.

Необходимо подчеркнуть, что смена дат при пересечении демаркационной линии - не догма, и необходима она только в случае, если при пересечении границ часовых поясов часы переставляются. Если же путешественник не переставляет часы, а живет по постоянному времени исходного пункта (или любого другого), то для него линии перемены дат просто не существует, поскольку у него дата будет меняться одновременно с полночью в исходном пункте - независимо от того, какому местному времени этот момент соответствует. Такой способ времяисчисления применяется, например, в арктических и антарктических экспедициях, поскольку в околополюсных зонах местное солнечное время уже не имеет особого практического значения, а на самих полюсах и вовсе не определено. А для космонавтов, находящихся на окоземной орбите, следование поясному времени и вовсе противоречит здравому смыслу - там переставлять часы пришлось бы примерно раз в 4 минуты, а даты - каждые полтора часа. Поэтому, например, на станция "Мир" всегда жила по московскому времени.

Однако вернемся на Землю. С 16 июля 1930 года специальным декретом правительства СССР все часы в стране переведены на 1 час вперед, и такое время получило название декретного времени. Сделано это в целях экономии электроэнергии в летний период. По декретному времени Солнце позже восходит и позже заходит, но в летний период большинство людей просыпается гораздо позже восхода, так что смещение захода на час дает возможность уменьшить расходы электроэнергии на освещение по вечерам, поскольку темнота наступает позже. Связь поясного (T_n) и декретного (T_д) времени на долготе l внутри часового пояса n (n^ч выражено в часах) со всемирным временем T₀ и средним местным временем T_m выглядит так:

T_n = T₀ + n^ч = T_m + n^ч - l (7)
T_д = T_n + 1^ч = T₀ + n^ч + 1^ч = T_m + n^ч - l + 1^ч (8)

С той же целью (экономии электроэнергии на вечернем освещении) ежегодно, начиная с 1981 года, вводится летнее декретное время. В начале весенне-летнего сезона часы переводятся еще на 1 час вперед, а по его окончании - обратно, на час назад. Сами сроки начала и окончания действия летнего времени неоднократно менялись. Так, в 1983 году оно вводилось с 1 апреля по 1 октября, в 1994 году - с 2 часов ночи последнего воскресенья марта по 3 часа ночи последнего воскресенья сентября, а в 1999 году - с 2 часов ночи последнего воскресенья марта по 3 часа ночи последнего воскресенья октября. Больше того, в последнее воскресенье марта 1991 года объявления о предстоящем очередном переходе на летнее время не последовало и часы на переставлялись. То ли в правительстве решили, что они умнее всех и пора избавиться от "предрассудков недавнего прошлого", то ли просто забыли о такой мелочи в политических игрищах. Такое бездействие можно также рассматривать и как введение летнего времени при одновременной отмене декретного. Особенно если учесть, что осенью 1991 года, как положено, время было переведено на 1 час назад. Как бы от ни было, но только 19 января 1992 года последовало постановление Правительства Российской Федерации о новом переводе времени на 1 час вперед. Тем самым было фактически восстановлено декретное время, и с тех пор подобных экспериментов больше не проводилось. Если не считать курьеза в Грузии, где 3 марта 2001 г. Эдуард Шеварнадзе подписал указ о переводе времени 25 марта 2001 г. на 1 час, но не вперед, как положено при весеннем переходе на летнее время, а назад! Правда, ошибка была вскоре замечена, и 10 марта последовал указ "противоположной направленности".

Таким образом, летнее время T_л выражается так:

Однако и это еще не все. В первой половине XX века были замечены расхождения между теоретическими и наблюдательными данными движения Луны, Меркурия и Венеры, причем эти расхождения можно было почти полностью устранить, если одинаково изменить все моменты времени в их эфемеридах. С появлением новых высокоточных часов было окончательно доказано, что эти расхождения вызваны неравномерностью вращения Земли. Если хорошие маятниковые часы дают за сутки погрешность в несколько сотых долей секунды, то есть их точность порядка 10^-7, то у появившихся в середине XX века кварцевых часов точность достигает 10^-9, а у современных молекулярных и атомных часов - 10^-13.

Таким образом, создание высокоточных часов позволило получить надежный эталон равномерного времени. Для достижения равномерности была введена новая шкала времени, основанная на стабильной единице длины, равной определенной части продолжительности 1900-го тропического года и названной эфемеридной секундой, а измеряемое таким образом время - эфемеридным временем. Нуль-пункт его выбран так, чтобы 1 января 1900 года эфемеридное время совпадало со всемирным. Со временем, из-за замедления вращения Земли, всемирное время стало отставать от эфемеридного. В среднем продолжительность одних суток увеличивается примерно на 0.0015 с за столетие, и к 1983 году это отставание достигло 55 с (с 1900 года прошло 83 года, а 83*0.0015*365.2422 ~ 45.5 с).

Однако происходит увеличение суток неравномерно. Наряду с общим замедлением происходят годичные колебания продолжительности суток. Так, ежегодно с июня по ноябрь вращение Земли немного ускоряется, а с ноября по июнь - замедляется, причем относительная величина этих колебаний достигает 10^-8. Вызваны они главным образом сезонными изменениями в земной атмосфере. Кроме того, наблюдаются и случайные изменения скорости вращения, которые могут быть связаны с изменениями распределения масс внутри Земли. Что касается общего векового замедления, его основная причина - действие приливных сил, при этом часть энергии вращения Земли переходит в тепловую энергию, а часть передается Луне. В результате происходит перераспределение момента импульса системы Земля - Луна: Луна постепенно удаляется от Земли и момент импульса Луны увеличивается, а Земли - уменьшается.

Эфемеридное время использовалось примерно до 1984 года. Развитие техники привело к созданию новой эталонной единицы времени - атомной секунды, равной 9192631770 переходам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния изотопа атома цезия ¹³³Cs. Основанная на атомной секунде шкала времени называется атомным временем, а ее нуль-пункт подобран таким образом, чтобы атомное время совпадало со всемирным временем около 1955 года. Погрешность измерения атомного времени - около 5*10^-14, и сигналы точного времени, транслируемые по радио, подаются именно с атомных часов.

Наконец, для компенсации неизбежного отставания всемирного времени от атомного, было введено всемирное координированное время, обозначаемое UTC или ВКВ. Оно также основано на атомной секунде, но числовое выражение подбирается так, чтобы оно отличалось от всемирного времени не более чем на 0.9 с, а от атомного времени - обязательно на целое число секунд. Из-за векового замедления вращения Земли всемирное время отстает от атомного примерно на секунду в год. Поэтому в среднем раз в год приходится смещать начало каких-либо календарных суток на одну секунду, о чем заранее объявляется. Именно значение UTC распространяется по радио в виде сигналов точного времени. Таким образом, всемирное координированное время является практически используемой модификацией атомного времени, однако фактически при этом некоторые сутки содержат на одну секунду больше (86401), чем остальные.

Однако и это еще не все. Уточнение теории движения Луны и планет и учет релятивистских поправок дали возможность ввести еще две новые шкалы времени: земное динамическое время (TDT) и барицентрическое динамическое время (TDB). Их появление связано с реализацией представлений теории относительности о действии гравитации на течение времени и были рекомендованы Международным астрономическим союзом в 1976 году. TDB употребляется для при построении теории движения тел Солнечной системы, TDT - для вычисления эфемерид явлений, наблюдаемых с Земли. Связь шкал TDT и TDB устанавливается теоретически на основе сведений о движении Земли и массах тел Солнечной системы. Для практических целей TDT можно рассматривать как продолжение эфемеридного времени. Земное динамическое время TDT связано со всемирным временем UT соотношением:

Наконец, в 1991 году Международный астрономический союз рекомендовал использовать еще три новые шкалы времени: барицентрическое координатное время TCB, геоцентрическое координатное время TCG и земное время ТТ. Эти времена отличаются из-за различия гравитационного потенциаля в центре масс Солнца, в центре масс Земли и на поверхности Земли. Практически в большинстве случаев земное время можно считать продолжением времени TDT. Земное время связано с UTC соотношением:

В Интернете точные времена можно всегда узнать, например, на сайте Heavens Above (после установки своего местоположения).

Год

Сутки, определяемые вращением Земли, служат основной единицей измерения коротких отрезков времени, но большие промежутки удобнее измерять более длинной единицей. Кроме того, повседневная деятельность человека тесно привязана не только к смене дня и ночи, но и к смене сезонов года. Поэтому продолжительность года, определяемая орбитальным вращением Земли вокруг Солнца, также является важной единицей времени.

Как и в случае с сутками, продолжительность года зависит от выбора метки, относительно которой определять годичное обращение Земли.

В качестве исходного направления можно выбрать прямую, проведенную из центра Солнца к далекой и поэтому практически неподвижной звезде (а еще лучше - внегалактическому объекту: галактике или квазару). Период обращения Земли относительно этого направления называется звездным или сидерическим годом и равен 365.25636 суток, что составляет 365 суток 6 часов 9 минут 10 секунд.

Однако смена сезонов года определяется видимым расположением Солнца относительно точек равноденствий, которые сами из-за прецесии смещаются навстречу Солнцу на 50" в год. Поэтому продолжительность года, определяемая по направлению на точку весеннего равноденствия, будет меньше звездного года. Промежуток времени между двумя последовательными прохождениями центра диска Солнца через точку весеннего равноденствия называется истинным или тропическим годом. Его продолжительность равна 365.2421988 суток (365 суток 5 часов 48 минут 46 секунд). Принимается, что и среднее солнце за это же время возвращается к точке весеннего равноденствия.

Введенные таким образом тропические годы имеют одинаковую продолжительность, в то время как календарные (о чем будет рассказано ниже) - то 365, то 366 суток. Для того, чтобы по возможности сблизить начала календарного и тропического годов, по предложению немецкого астронома Ф.В.Бесселя (1784-1846) за начало астрономического (тропического) года принимают момент, когда прямое восхождение среднего экваториального солнца равно 18^ч40^м. Отсчитываемый от этого момента тропический год называется бесселевым годом. Моменты его начала приводятся в астрономических ежегодниках.

Кроме того, продолжительность года можно определить и относительно прохождения Землей ближайшей к Солнцу точки своей орбиты - перигелия. Такой год называется аномалистическим годом, его продолжительность составляет 365.25964 суток (365 суток 6 часов 13 минут 53 секунды), что на 4 минуты 43 секунды больше, чем длина звездного года. Эта разница вызвана медленным смещением точки перигелия в направлении орбитального движения Земли.

Наконец, можно определить период орбитального движения Земли относительно лунных узлов - точек пересечения плоскости лунной орбиты с проскостью эклиптики. Такой год получил название драконического года и с ним связаны солнечные и лунные затмения. Поскольку лунные узлы сравнительно быстро (с периодом 18.6 лет) смещаются по эклиптике, то драконический год значительно короче остальных и составляет всего 346.62003 суток (346 суток 14 часов 52 минуты 51 секунда).

Следует подчеркнуть, что абсолютное значение продолжительности года связано только с орбитальным движением Земли и со временем не меняется. Однако, как упоминалось выше, продолжительность суток медленно увеличивается, и поэтому число суток, содержащихся в тропическом году, должно медленно, но неуклонно уменьшаться. Этот эффект приближенно описывается формулой С.Ньюкома.

Так, тропический год, выраженный в продолжительности суток, будет равен:

в 3000 г. до н.э.            365.242500 суток

в 1 г. н.э.                  365.242316 суток

в 1900 г. н.э.               365.242199 суток

в 4000 г. н.э.               365.242070 суток

В настоящее время величина тропического года (выраженная в текущей продолжительности суток) уменьшается каждое столетие на 0.54 секунды. Миллиард лет назад назад сутки были примерно на 4 часа короче, чем сейчас, а через 4.5 млрд. лет за год Земля будет делать всего 9 оборотов вокруг оси.

Лунный месяц

Третья природная единица измерения времени связана с орбитальным движением Луны. Наблюдаемое перемещение Луны по небесной сфере в целом подобно перемещению Солнца (см. главу "Эклиптическая система координат ..."), но совершается намного быстрее. Кроме того, лунная орбита наклонена к плоскости эклиптики на угол 5^o9', а точки их пересечения (лунные узлы) непрерывно смещаются навстречу Луне (то есть к западу) примерно на 20^o в год, делая полный оборот за 18.61 года. К тому же лунная орбита имеет заметный эксцентриситет (e ~ 0.0549), а близость Луны к Земле вызывает значительное параллактическое смещение первой.

Как и в предыдущих случаях, период обращения Луны также можно измерять по отношению к разным начальным направлениям.

Наблюдая за положением Луны на небе, можно убедиться, что помимо участия в общем суточном вращении небесной сферы с востока на запад она также перемещается среди звезд с запада на восток (в ту же сторону, что и Солнце) со средней скоростью 13^o.2 в сутки, или на 33' в час (что почти равно ее видимому диаметру). Сделав полный круг на небесной сфере, спустя 27.321661 суток (27 суток 7 часов 43 минуты 11.5 секунд) Луна возвращается к исходному направлению на далекую (неподвижную) звезду. Этот промежуток времени называется сидерическим месяцем.

Поскольку Луна светит отраженным светом, то при ее обращении вокруг Земли изменяется положение Солнца относительно полушария Луны, обращенного к Земле. Вследствие этого меняется и освещенность этого полушария, что приводит к периодической смене фаз Луны. Промежуток времени, спустя который фазы Луны снова повторяются в том же порядке, называется синодическим месяцем. Он равен 29.530588 суток (29 суток 12 часов 44 минуты 2.8 секунды). Однако это среднее значение, поскольку из-за эллиптичности орбиты линейная и наблюдаемая угловая скорости движения Луны различны в разных точках орбиты. Например, угловая скорость изменяется в пределах от 11^o до 15^o в сутки. Кроме того, на движение Луны оказывает влияние и притяжение Солнца. В результате реальная продолжительность синодического месяца меняется от 29^д 6^ч 15^м до 29^д 19^ч 12^м.

Как и в случае с орбитальным движением Земли, перемещение Луны также можно определить относительно точек равноденствия (тропический месяц, равный 27.32158 суток), точки перигея (аномалистический месяц, равный 27.55455 суток) и лунных узлов (драконический месяц, равный 27.21222).

В повседневной жизни наиболее удобным и практичным периодом обращения Луны является период смены ее фаз - синодический месяц. Однако использовать его для построения календаря не так просто, как кажется на первый взгляд. Прежде всего, за исходную фазу логичнее всего было бы принять полнолуние, однако определить на глаз момент полнолуния очень сложно, поскольку Луна в этой фазе 2-3 суток подряд выглядит одинаково полной.

Другая применявшаяся точка отсчета - первое после новолуния появление Луны на вечернем небе, называемое неоменией. От неомении и было удобнее всего начинать счет времени в месяце. Однако продолжительность синодического месяца может быть на 6 часов меньше или больше среднего значения, поэтому и неомения может наступить как днем раньше, так и днем позже по отношению к средней дате. Кроме того, время первого появления лунного серпа на вечернем небе сильно зависит от условий наблюдений, в первую очередь - от наклона эклиптики к горизонту в этот момент. Весной, после захода Солнца, над горизонтом находится северная часть эклиптики, поэтому вечерняя Луна располагается выше небесного экватора. А потому и заходит она позже, и, следовательно, на фоне более темного неба ее заметить гораздо легче, чем осенью на таком же угловом расстоянии от Солнца. Этот эффект к тому же усиливается наклоном лунной орбиты к эклиптике, благодаря чему угол между плоскостями лунной орбиты и небесного экватора меняется с периодом 18.6 лет от 18^o.5 до 28^o.5, а вместе с ним меняется и высота над западным горизонтом серпа Луны. Наконец, расположение эклиптики относительно горизонта зависит от широты места наблюдения, и вышеизложенное гораздо сильнее проявляется в средних широтах, чем в южных. В результате весной складываются более благоприятные условия для наблюдений вечерней Луны, и поэтому ее серп можно заметить на сутки раньше, чем осенью.

Юлианский календарь

Календарь можно определить как систему счета продолжительных промежутков времени, согласованную с периодически повторяющимися природными явлениями - смена дня и ночи, лунных фаз и времен года. Однако продолжительность суток, синодического месяца и тропического года несоизмеримы между собой, и поэтому создать на их основе простой и точный календарь не представляется возможным. Использовавшиеся в разные эпохи разными народами календари можно разделить на три типа. Лунные календари делили год на определенное (например, 12) число месяцев, продолжительность каждого из которых была близка к синодическому месяцу, не принимая во внимание их расположение по временам года. Солнечные календари за основу счета дней принимали смену времен года, без учета фаз Луны. Наконец, солнечно-лунные календари сочетали счет времени по лунным месяцам и согласование продолжительности года со сменой времен года, поэтому отличались особой сложностью.

Праобраз современного календаря ввел в 46 г. до н.э. римский полководец и писатель Гай Юлий Цезарь (100-44 гг. до н.э.), для чего были использованы знания египетских астрономов (к разработке нового календаря был привлечен александрийский астроном Созиген). В его основу был положен солнечный год, продолжительность которого была принята равной 365.25 суток. Поскольку календарный год может содержать только целое число суток, то из каждых четырех лет три имели продолжительность 365 суток, а четвертый - 366. Год с дополнительным днем позже был назван annus bissextus, откуда и произошло современное название "високосный".

Дореформенный древнеримский календарь был лунно-солнечным, и в нем первые числа каждого месяца назывались календами ("календариум" - долговая книга, в эти дни выплачивали проценты по долгам). Название сохранилось и после реформы, откуда и произошло само слово календарь. Хотя новый календарь стал чисто солнечным, в нем от старого лунно-солнечного календаря сохранилось разделение на месяцы - они стали единицами внутренней структуры солнечного года, хотя и потеряли связь с реальным фазами Луны.

В реформированном календаре год разделялся на 12 месяцев, названия которых были перенесены из древнеримского календаря: Мартиус (в честь бога войны Марса), Априлис (от aperire - "раскрывать" или apricus - "согреваемый Солнцем"), Майус (в честь богини земли Майи), Юниус (в честь богини неба Юноны), Квинтилис (пятый), Секстилис (шестой), Септембер (седьмой), Октобер (восьмой), Новембер (девятый), Децембер (десятый), Януариус (в честь бога Януса) и Фебруариус (в честь бога подземного царства Фебрууса). До реформы год начинался с 1 марта, поэтому названия месяцев с пятого по десятый просто отображали их порядковый номер.

В новом календаре Юлий Цезарь упорядочил также число дней в месяцах таким образом, чтобы нечетный месяц содержал 31 день, четный - 30. Только февраль в простом году должен был иметь 29 дней, в високосном - 30. Кроме того, начало года было перенесено на 1 января, которое в 45 г. до н.э. как раз совпало с новолунием. Через два года Юлий Цезарь был убит, и в благодарность за реформу календаря и военные заслуги римский сенат переименовал месяц Квинтилиус, в котором Цезарь родился, в Юлиус. А позже и сам введенный календарь, счет по которому был начат с 1 января 45 г. до н.э., получил название юлианского.

Однако вскоре високосным стал объявляться не каждый четвертый, а каждый третий год, и с 44 по 9 гг. до н.э. было введено 12 високосных годов сместо положенных 9. Эту ошибку исправил император Август, по инициативе которого на протяжении последующих 16 лет (с 9 г. до н.э. по 8 г. н.э.) високосных годов не было. В результате юлианский календарь фактически начал нормально функционировать с 1 марта 4 г. н.э. В благодарность за исправление календаря и опять-таки за военные заслуги сенат переименовал месяц Секстилиус в Августус. Однако поскольку в этом месяце было всего 30 дней, то к нему добавили еще один, отнятый от Фебруариуса. А чтобы три месяца подряд (Юлиус, Августус и Септембер) не содержали по 31 день, то от Септембера один день был перенесен на Октобер, а от Новембера - на Децембер. В результате было нарушено введенное Цезарем правильное чередование длинных и коротких месяцев, а первое полугодие в простом году оказалось на 4 дня короче второго, что вместе с римскими названиями месяцев сохранилось до настоящего времени.

История последней единицы внутренней структуры календаря - недели - не менее интересна. Обычай измерять время семидневными неделями пришел из Древнего Вавилона и, скорее всего, также связан с лунными фазами - как следствие разделения лунного месяца на 4 части. При точном следовании фазам Луны неделя должна была содержать то 7, то 8 дней (поскольку 1/4 от синодического месяца составляет 29.53059/4 ~ 7.383 суток), и впоследствии (по-видимому, для удобства) ее приняли 7-дневной. Кроме того, числу 7 приписывались магические свойства - в частности, было известно 7 планет (включая Солнце и Луну).

Возникшая в Древнем Вавилоне астрология связывала судьбы отдельных людей и целых народов с влиянием планет. Разделив сутки на 24 часа, астрологи утверждали, что каждый час суток находится под покровительством определенной планеты. Счет часов был начат с субботы, ее первым часом "управлял" Сатурн, вторым - Юпитер, третьим - Марс, четвертым - Солнце, пятым - Венера, шестым - Меркурий, и седьмым - Луна (в порядке убывания расстояний до Земли, по представлениям того времени). Далее этот цикл повторялся, так что Сатурн "управлял" 8-м, 15-м и 22-м часами, Юпитер - 9-м, 16-м и 23-м, и т.д. По такой схеме получилось, что 1-м часом первого дня "управлял" Сатурн, второго - Солнце, третьего - Луна, четвертого - Марс, пятого - Меркурий, шестого - Юпитер, седьмого - Венера. Дни недели получили названия соответственно "своим" планетам, затем эти названия перешли в римский календарь, а из него - в календари многих народов Европы, часто с некоторыми изменениями. Например, англичане взяли названия для вторника, среды, четверга и пятницы из скандинавской мифологии, в которой Тиу соответствует Марсу, Водан - Меркурию, Тор - Юпитеру, Фрейя - Венере. Отсюда и современные английские названия: "Tuesday", "Wednesday", "Thursday" и "Friday". Остальные три дня переводятся традиционно: "Saturday" - день Сатурна, "Sunday" - день Солнца, "Monday" - день Луны.

Помимо связи с названиями планетами, во многих языках некоторые дни недели (а иногда и все) получали названия соответственно их порядковому номеру в неделе. Нумерация дней, начиная с воскресенья, берет начало также в Древнем Вавилоне. В славянских языках некоторые дни недели также были пронумерованы, и их счет велся, начиная с воскресенья (например, у мусульман первым днем считается суббота). Воскресенье у славян называлось неделей, т.е. днем, когда ничего не делают (днем отдыха), и это название сохранилось во всех славянских языках, кроме русского. В русском языке название "неделя" перешло на всю семидневку, а следующие пять дней расшифровываются очень просто: понедельник - первый день после недели, вторник - второй, среда - средний день (в старославянском языке есть ее более древнее название - третийник), четверг - четвертый, пятница - пятый. День Сатурна у вавилонян считался несчастливым, и в этот день предписывалось не заниматься никакими делами, он был перенесен в конец недели и получил название "шаббат", что значит - покой. Это название перешло в еврейский, арабский, славянские и некоторые западноевропейские языки, так объясняется и происхождение слова "суббота". Современное название последнего дня (воскресенья) установилось под влиянием христианства - как день воскрешения Иисуса Христа.

Семидневная неделя распространилась по Римской Империи еще при императоре Августе, в связи с увлечением римлян астрологией. Окончательно она установилась с 321 года, когда день Солнца (воскресенье) был официально утвержден римским императором Константином как еженедельный государственный праздник.

Григорианский календарь

Юлианский календарь оказался весьма привлекательным и применялся полтора тысячелетия благодаря своей простоте и строгой ритмичности смены простых и високосных годов. Каждые четыре года содержат 1461 сутки, каждое столетие - 36525 суток. Поэтому такая система счета была очень удобной для измерения длительных интервалов времени. Однако средняя продолжительность юлианского календарного года больше тропического года на 365.25 - 365.2422 = 0.0078 суток, что составляет примерно 11 минут 14 секунд. Поэтому юлианский календарь отстает от астрономического - например, каждый простой год весеннее равноденствие по такому календарю сдвигается на 0.2422 суток вперед, а каждый високосный - на 0.7578 суток назад, и к концу каждого четырехлетнего цикла - на 0.0312 (0.0078*4) суток назад. Расхождение в 1 сутки накапливается за 128 лет. Если в начале нашей эры весеннее равноденствие происходило 23 марта, то спустя 400 лет - на трое суток раньше, то есть на 20 марта. Таким образом, по отношению к определенным временам года юлианский календарь уходит вперед, а относительно дат этого календаря астрономические явления сдвигаются назад.

Со времени Юлия Цезаря до Никейского Собора (325 г.) накопилось расхождение в трое суток, впоследствии чего астрономический момент весеннего равноденствия переместился с 24 марта на 21. Никейский Собор утвердил 21 марта днем весеннего равноденствия, однако поскольку причина расхождения устранена не была, к концу XVI века дата весеннего равноденствия сместилась на 10 суток, с 21 на 11 марта. В 1582 году католическая церковь провела реформу календаря с восстановлением даты весеннего равноденствия 21 марта, для чего следующий после 4 октября 1582 года день был объявлен 15 октября. В честь осуществившего эту реформу римского папы Григория XIII введенный календарь был назван григорианским.

В григорианском календаре простой год также содержит 365 суток, високосный - 366, и високосным также считается каждый четвертый год - тот, номер которого в нашем исчислении делится на 4 без остатка. Однако для устранения причины неточности юлианского календаря из григорианского каждые 400 лет дополнительно выкидываются еще 3 дня, для чего вековые годы, в которых число сотен не делится на 4 без остатка (например, 1700, 1800, 1900, 2100), считаются не високосными, а простыми. Полный цикл такого календаря составляет 400 лет и содержит 303 простых года и 97 високосных, а в сумме - 146097 суток (интересно, что первый такой цикл после введения этого календаря закончился совсем недавно - 15 октября 1982 года). Средняя продолжительность григорианского календарного года равна 365.24250 суток, что больше тропического года всего на 0.00030 суток (26 секунд). Ошибка в одни сутки накапливается за 3300 лет, и благодаря простоте системы високосных годов григорианский календарь считается весьма удачным. Интересно отметить, что приведенное расхождение григорианского календаря с астрономическим со временем будет медленно увеличиваться, поскольку григорианский год уже длиннее тропического, а последний из-за замедления вращения Земли медленно уменьшается в пересчете на сутки. А раз так, то раньше разность между ними была меньше, а когда-то они даже были в точности равны! Продолжительности тропического года в разные эпохи уже приводились в разделе "Год", и значение 365.2425 суток соответствует эпохе 3000 г. до н.э.! То есть для Древнего Египта григорианский календарь (по средней продолжительности календарного года) подошел бы идеально! Аналогично по приведенной формуле С.Ньюкома можно вычислить, когда тропический год соответствовал бы простому юлианскому календарю, но получится весьма древняя эпоха - порядка 130 тыс. лет назад.

Нужно иметь в виду, что хотя в среднем в 400-летнем григорианском цикле продолжительность календарного года хорошо согласована с длиной тропического года, календарная ошибка, исправляемая вставками високосных годов, распределяется от года к году неравномерно. А именно - в периоды вековых невисокосных годов бывает по 7 простых годов подряд. Как было упомянуто выше, каждый простой год сдвигает момент весеннего равноденствия на 0.2422 суток вперед, а за 7 лет смещение составит 0.2422*7 = 1.6954 суток! Благодаря этому, например, в 1896 г. равноденствие было 20.05 марта, а в 1903 - 21.75 марта. В первой половине XX века равноденствие приходилось чаще на 21 марта, а во второй - на 20. Кроме того, из-за неточности григорианского календаря весеннее равноденствие в 2000 году наступило на 0.12 суток раньше, чем в 1600.

Следует подчеркнуть, что именно простота григорианского календаря является его главным достоинством. Применяя более сложные правила исключения лишних дней из юлианского календаря, можно создать более точную, чем григорианская, систему счета. Например, если каждый восьмой четырехлетний цикл увеличить на один год, т.е. принять, что в нем четыре простых года и один високосный, то каждые 33 года будут состоять из 25 простых и 8 високосных, и неточность юлианского календаря будет погашаться в пределах 33 лет, а расхождение в 1 сутки относительно астрономического года накопится за 4400 лет. Такую систему високосных годов применил в XI веке иранский ученый и поэт Омар Хайям. Еще более точным является проект, предложенный в 1864 году астрономом И.Мэдлером, согласно которому нужно исключать один високосный год каждые 128 лет, и тогда расхождение в 1 сутки накопится только через 86.4 тыс. лет. Однако такие варианты уступают григорианскому календарю с точки зрения простоты и удобства.

Введение григорианского календаря, сопровождаемое пропуском 10 суток, привело к сосуществованию двух летоисчислений - "старого стиля" (юлианского) и "нового стиля" (григорианского). Причем сосуществованию на протяжении трех столетий, поскольку в разных странах григорианская эпоха была принята в разные годы, в первую очередь - там, где было преобладающим влияние католической церкви. И задержка реформы в ряде стран была вызвана именно необоснованным смещением дат, чем был внесен разлад в хронологию и повседневную жизнь. Поскольку совершенно безразлично, к какой календарной дате будет привязано опорное астрономическое явление, то пропуск 10 дней в григорианской реформе можно считать нерациональным шагом. Как известно, Россия перешла на новый стиль только в 1918 году, когда его расхождение со старым стилем составило 13 дней. Эта разница сохранится и в XXI веке (поскольку 2000 год был високосным как в григорианском, так и в юлианском календаре, а поэтому нет и причины изменения расхождение между ними), и только начиная с марта 2100 года разница между новым и старым стилем увеличится до 14 суток.

Также достойно внимания, что внутренняя структура годового календаря (его разбивка на месяцы и недели) подчиняется определенным закономерностям, используемым при составлении обзорных или "вечных" календарей - вычислительных приспособлений, позволяющих определить день недели для любой даты в прошлом и будущем.

Прежде всего, поскольку 365 = 7*52 + 1, то очевидно, что простой год всегда заканчивается тем же днем, с которого начинается, а високосный - следующим. Поэтому каждый год день недели, приходящийся на 1 января, смещается на один день недели вперед по отношению к 1 января предыдущего года, если последний был простым, а если високосным - то на два дня. Таким образом, дни недели каждый год смещаются относительно чисел месяцев (и праздничных дней) - на один или два дня. Нетрудно также догадаться, что по дню недели, приходящемуся на 1 января, существует всего 14 вариантов годовых календарей - 7 для простых лет и 7 для високосных. Аналогично возможно 28 вариантов распределения дней недели по месяцам - по семь для месяцев с 28, 29, 30 и 31 днями. 14 вариантов годовых календарей также объединяются в 28-летние циклы с 7 високосными годами и 21 простыми (каждый из вариантов простых годов появляется в цикле трижды, високосных - по одному разу), и каждые 28 лет календарный порядок следования вариантов полностью повторяется. Этот порядок нарушается только при переходе через вековой невисокосный год. Например, с понедельника начинались невисокосные годы 1945, 1951, 1962, 1973, 1979, 1990 и 2001 - первый из любой тройки отделен от первого в следующей тройке как раз на 28 лет.

Стиль летоисчисления имеет и другой смысл - определение начала года. В этом смысле и юлианский, и григорианский календари - январские, поскольку новый год в них начинается с 1 января.

Системы летоисчисления

Помимо продолжительности календарного года важное значение имеет и "точка отсчета" годов - начало календарной эры. Это начало обычно связывалось с какам-либо историческим событием, реальным или мифическим. Например, в Древнем Вавилоне применялась эра от начала царствования Набонассара - 747 г. до н.э., в Древней Греции - от начала первой олимпиады - 776 г. до н.э., в Древнем Риме - от даты основания Рима Ромулом - 753 г. до н.э., а позднее - от начала правления императора Диоклетиана - 284 г. до н.э. Существует также несколько вариантов эры от "сотворения мира": 3761 г. до н.э. по древнееврейскому календарю и 1 марта 5508 г. до н.э. - по византийскому (она называется также константинопольской или древнерусской), и "сентябрьский вариант" - 1 сентября 5509 г. до н.э.

Современное летосчисление "от рождества Христова", назаваемое "нашей эрой", было введено в 525 году римским монахом Дионисием Малым на основании проведенных им вычислений. В XVIII веке эра, установленная Дионисием, была расширена и для счета лет до "рождества Христова". При этом было принято, что перед 1-м годом н.э. расположен 1-й год до н.э., а номер года до н.э. возрастает возрастает по мере удаления в прошлое (хотя месяцы, числа месяцев и дни недели расположены в них в обычном порядке). Високосными являются те годы до н.э., номер которых при делении на 4 дает в остатке 1: 5-й, 9-й, 13-й и т.д. Такой счет лет называется историческим или хронологическим. Отсутствие нулевого года часто приводит к ошибкам в вычислениях интервала времени между двумя событиями, если одно из них произошло до н.э., а другое - в нашей эре. Еще одно недавнее "последствие" начала нашей эры с 1-го года - амбициозные празднования вступления в XXI век и 3-е тысячелетие, предпринятые в ряде стран 1 января 2000 года, тогда как на самом деле с 1-го года до 2000-го прошло только 1999 лет, и поэтому 2000 год является не первым годом XXI века, а последним годом XX века. XXI же век, согласно принятой системе летоисчисления, начался 1 января 2001 года, что, конечно, уже не так привлекательно по причине "некруглости" этого года по сравнению с числом 2000.

Существует также и астрономическая система счета, впервые использованная в 1740 году французским ученым Жаком Кассини (1677-1756). В ней год, предшествовавший 1-му году н.э., был назван нулевым, перед нулевым шел минус первый, и т.д. Так появилось "правило Кассини": для определения отрезка времени между между двумя событиями, разделенными точкой начала нашей эры, номер года до н.э. при вычитании необходимо уменьшать на единицу.

Наконец, в астрономических и хронологических расчетах часто используется непрерывный счет дней, начиная от 1 января 4713 г. до н.э., называемый юлианским периодом и введенный в 1583 г. французским ученым Жозефом Скалигером (1540-1609). Порядковый номер дня в этом счете называется юлианской датой и сокращенно обозначается Ю.Д. или JD. За начало юлианской даты принимается средний полдень на нулевом (гринвичском) меридиане (до 1925 года за начало средних солнечных суток принимался именно средний полдень - см. определение среднего солнечного времени). Поэтому в системе юлианских дней сутки отсчитываются от среднего гринвичского полудня, следующего за средней гринвичской полуночью, с которой начинается рассматриваемая календарная дата. Приведенное правило нужно помнить при пользовании таблицами юлианских дат, которые размещаются в астрономических календарях и прочих печатных изданиях, поскольку для конкретных дат обычно приводятся целые юлианские дни. Однако в настоящее время в научных изданиях юлианскую дату часто приводят с дробной частью, представляющей из себя всемирное время рассматриваемого момента, выраженное в долях суток. Например, 0 часов 1 января 2000 г. соответствует юлианской дате 2451544.5.

Обычная юлианская дата имеет 7 цифр до запятой, и для небольших промежутков времени (например, нескольких десятилетий) несколько первых цифр не меняются, и оттого использование полного номера юлианского дня становится нерациональным. Поэтому существует несколько модификаций юлианских дней, которые сохраняют их основной принцип - порядковый номер суток, начиная с определенной даты, но начальная дата выбирается гораздо ближе к современной эпохе, что позволяет существенно сократить номер дня и тем самым сделать его использование более удобным. Эти модификации в основном делятся на два типа. Первый - сделать начальным днем какую-нибудь круглую календарную дату: чаще всего это 0.5 января 1950 года (то есть 31.5 декабря 1949 года) или 0.5 января 1900 года. Эти системы, а особенно - первая из них, называется модифицированной юлианской датой и обозначается MJD, и 0 часов 1 января 2000 года будет иметь в этих системах номера соответственно 18262.5 и 36524.5. Второй путь - вычесть из обычной юлианской даты круглое число, обычно с добавлением 0.5, чтобы откинуть несколько первых цифр и получить для начала суток целое число. Чаще всего вычитают 2400000.5 или 2440000.5 - в первом случае просто отбрасываются две первые цифры, а во втором - для современной эпохи номер дня становится заведомо меньше 32000, что, помимо прочего, небезразлично и для компьютерных вычислений (в ряде языков программирования не придется заводить переменные с удвоенной точностью).

При точных вычислениях необходимо также помнить о разнице между строго равномерным атомным временем и всемирным координированным временем, согласованным с вращением Земли, но неравномерным. Как уже упоминалось, примерно раз в год начало определенных календарных суток приходится смещать на 1 секунду, и если, например, вычистяется точный интервал времени между двумя событиями, находящимися по разные стороны от такого смещения, то физически этот интервал будет на 1 секунду (или несколько секунд, если было несколько передвижек) длиннее, чем следует из простого пересчета дат. А все потому, что сутки, предшествовавшие смещению времени, будут содержать не стандартное число секунд (86400), а на одну больше.

Измерение времени и календарь

Николай Александрович

Сутки

Год

Лунный месяц

Юлианский календарь

Григорианский календарь

Системы летоисчисления